Every once in a while, it’s good to look at things from a different perspective, especially if you’re stuck in a rut. In this post, we look at the mathematics of melody, or rather we’ll be using math to uncover the melodic possibilities of a set of intervals. As we shall see, and before you run for the hills, this is going to be somewhat reassuring, especially if you’d ever thought there was nothing new under the sun. A while ago we looked at a system for creating melodic guitar solos, which turned into the book, ‘Melodic Soloing in 10 Days’. What we’re going to cover here would be a great extension to the ground covered in this book. Let’s check it out.
I’d always found Allan Holdsworth’s comment about first trying to permutate intervals with math really intriguing, and it wasn’t until I started to do the same that I could see where he was coming from. I started with major and minor triads, which have three intervals. The major triad has the intervals 1, 3 and 5. Here they are on the fretboard in G:
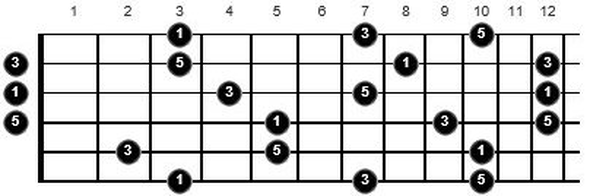
If you have three different notes, there are six possible permutations:
1 3 5
1 5 3
3 1 5
3 5 1
5 1 3
5 3 1
Here’s a G minor triad all over the fretboard:
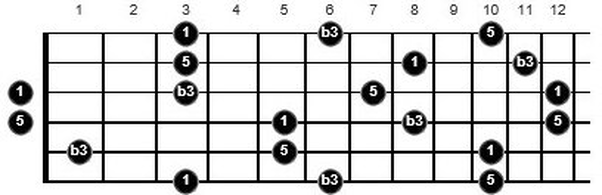
Again, there are six possible permutations:
1 b3 5
1 5 b3
b3 1 5
b3 5 1
5 1 b3
5 b3 1
What’s the Point?
From a teaching point of view, this makes for a great exercise to practice making melodies. Just use the different permutations to come up with melodic soloing ideas!
Arpeggios
If we add one note to either of the above triads, we get a seventh arpeggio which is the intervals of a seventh chord played as single notes. Let’s see what happens when we permutate an arpeggio. Here’s a G7 arpeggio all over the neck:
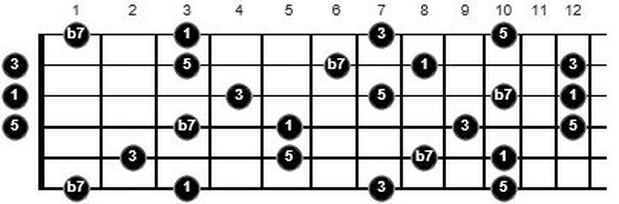
We now have four different intervals (1, 3, 5, b7), and permutating four intervals gives us 24 possibilities for melodic combinations as follows:
1 3 5 b7
1 3 b7 5
1 5 3 b7
1 5 b7 3
1 b7 3 5
1 b7 5 3
3 1 b7 5
3 1 5 b7
3 5 b7 1
3 5 1 b7
3 b7 5 1
3 b7 1 5
5 1 3 b7
5 1 b7 3
5 3 1 b7
5 3 b7 1
5 b7 1 3
5 b7 3 1
b7 1 5 3
b7 1 3 5
b7 3 5 1
b7 3 1 5
b7 5 3 1
b7 5 1 3
If you’re a little masochistic you could do the same exercise we did for the triads, or just the first ten or so permutations.
Pentatonics
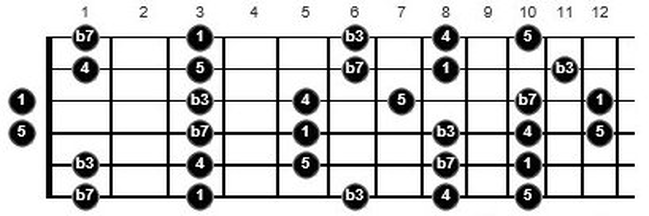
Here’s where it starts to get (more) interesting. If we take five notes i.e. a pentatonic scale such as G minor pentatonic below, we get 120 melodic permutations of intervals, and one hell of an exercise!
Seven-note Scales
The difference in melodic possibilities between a pentatonic scale and a seven-note scale is quite something and may explain why everyone sounds the same when they play a pentatonic scale. If we take a seven-note scale such as G natural minor (below), we generate 5,040 possible permutations! Quite a few more than the trusty old pentatonic scale.
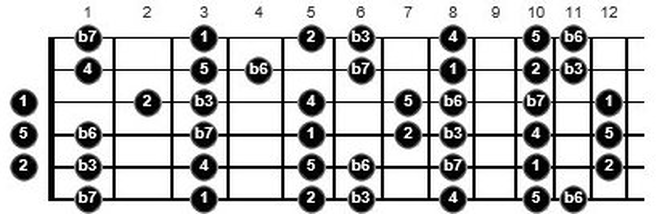
And if you’re curious, a group of 8 intervals generates 40,320 permutations! I’ll leave you to draw your own conclusions. Do practice the permutations for triads and seventh chord arpeggios though, as these as good for your fingers as they are for your ears, and when you add in the rhythmic possibilities, perhaps you’ll find that there is something new under the sun.



